再帰型プログラミングの試み

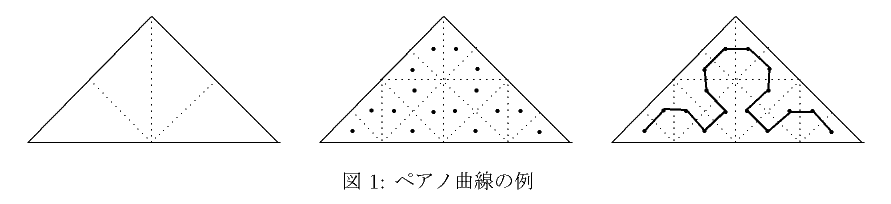
1. Example of Peano curve

　図１左のように三角形を分割し4個の領域に分ける．区分された三角形を更に4個に分割を繰り返す。得られた各小三角形の重心は図１中に示されている。これらの点16個を次々につなぐと図１右のような曲線が得られる。これがペアノ曲線（注１）の一例である。

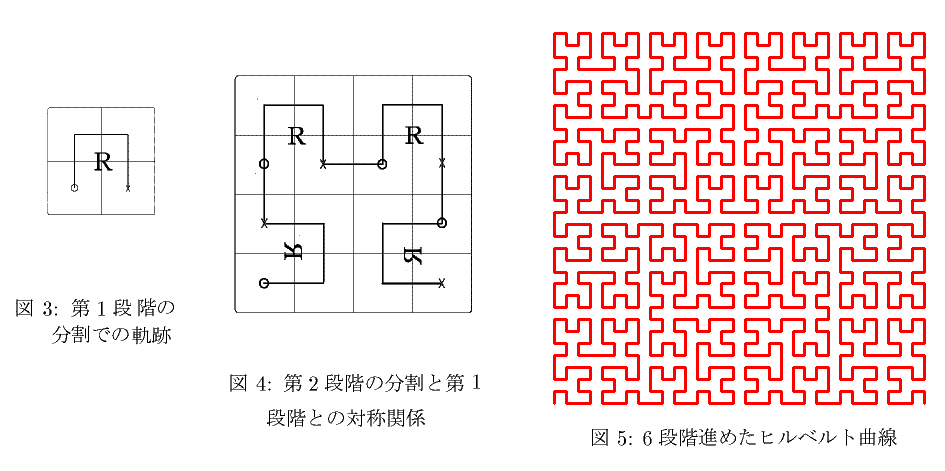
以下のようなFull BASIC(注２) による再帰型SUBプログラムPeano(n)（注３）によって容易にペアノ曲線が得られる。図２は正方形の対角線で得られる2つの三角形のそれぞれを5回分割を繰り返して得られたものである。この閉じた曲線をシェルピンスキー曲線という。閉じた曲線を示すために線の内部が塗りつぶされている。

OPTION ANGLE DEGREES PICTURE Peano(n) IF n=1 THEN PLOT LINES: 1.0, 0.3333 ; ELSE DRAW Peano(n-1) WITH SCALE(1/2) DRAW Peano(n-1) WITH SCALE(1/2)*ROTATE(90)*SHIFT(1,0) DRAW Peano(n-1) WITH SCALE(1/2)*ROTATE(-90)*SHIFT(1,1) DRAW Peano(n-1) WITH SCALE(1/2)*SHIFT(1,0) END IF END PICTURE SET WINDOW -0.1,1.6,-0.1,1.6 SET BEAM MODE "IMMORTAL" LET s2=SQR(2) DRAW Peano(5) WITH ROTATE(45) DRAW Peano(5) WITH ROTATE(-135)*SHIFT(s2,s2) PLOT LINES : 0.0295,0.059 PAINT 0.032,0.059 END

注１　Giuseppe Peano\ (1858〜1932), イタリアの数学者，記号論理学の開拓者．1890年に彼によって提案された。
注２　http://hp.vector.co.jp/authors/VA008683/
注３　上のHome Pageにあるインストーラ版を展開すると，各種プログラムが「SAMPLE」等から得ることができる。

2.　Hilbert curve

　ヒルベルト曲線は次のような考察によって，ペアノ曲線と同様に再帰型SUBプログラムを実行することによって得られる。
　図４のように正方形の領域を4分割し、各小正方形の中心を印○から始め印Xまで線を引きコの字型を描く。中心には対称性を明示するためにアルファベットの「R」が示されている。更に分割を進めると図５が得られる。各小正方形の中心には軌跡と同じ対称関係にある「R」が示されている。


図５は6段階分割を進めて描かれたものである。それを描くためのFull BASIC プログラムは以下のごとくである。再帰型SUBプログラムには上に示された「R」の対称関係が考慮されている．